Discriminant

En mathématiques, le discriminant noté ${\displaystyle \Delta }$, ou le réalisant noté ${\displaystyle \rho }$, est une notion algébrique. Utilisé pour résoudre des équations du second degré, il se généralise pour des polynômes de degré quelconque et dont les coefficients sont choisis dans des ensembles munis d'une addition et d'une multiplication. Le discriminant apporte dans ce cadre une information sur l'existence ou l'absence de racines multiples.

Le discriminant est utilisé dans d'autres domaines que celui de l'étude des polynômes. Son usage permet de mieux comprendre les coniques et les quadriques en général. On le retrouve dans l'étude des formes quadratiques, dans celle des corps de nombres dans le cadre de la théorie de Galois, et dans celle des nombres algébriques. Sa définition se fonde sur le calcul d'un déterminant.

Historique

L'histoire et la découverte du discriminant est un élément de l'histoire plus générale de l'algèbre et en particulier de la résolution des équations du second degré. Il apparait notamment lorsqu'on résout ces équations à l'aide d'identités remarquables.

Polynômes du second degré

Résolution de l'équation à coefficients réels

Considérons une équation du second degré, ici ${\displaystyle a}$, ${\displaystyle b}$ et ${\displaystyle c}$ sont trois coefficients réels tel que ${\displaystyle a}$ est différent de zéro :

${\displaystyle ax^{2} bx c=0}$

La connaissance du discriminant permet de résoudre l'équation :

Dans ce dernier cas, le discriminant a toutefois une racine complexe et donc une solution complexe.

Résolution de l'équation à solutions ou coefficients complexes

Si les solutions en nombres complexes de l'équation sont admises, ou plus généralement si les coefficients ${\displaystyle a}$, ${\displaystyle b}$ et ${\displaystyle c}$ sont complexes, la situation est un peu différente. Le théorème de d'Alembert-Gauss précise qu'il existe toujours au moins une solution à l'équation. Dans l'ensemble des complexes, un nombre admet toujours deux racines carrées, il existe une valeur ${\displaystyle \delta }$ telle que ${\displaystyle \delta ^{2}=\Delta }$ :

Discriminant réduit

Le discriminant réduit apparait quand on écrit l'équation du second degré sous la forme :

${\displaystyle ax^{2} 2b'x c=0}$

par un changement de variable ${\displaystyle b'={\frac {b}{2}}}$. Dans ce cas les 2 et 4 apparaissant dans l’expression des solutions et du discriminant se simplifient et on obtient :

L'expression des racines, si elles existent, devient :

${\displaystyle x_{1}={-b^{\prime } \delta ^{\prime } \over a}\quad {\text{et}}\quad x_{2}={-b^{\prime }-\delta ^{\prime } \over a}\quad {\text{avec}}\quad {\delta ^{\prime }}^{2}=\Delta ^{\prime }={b^{\prime }}^{2}-ac}$

Exemples

Cherchons à résoudre l'équation suivante :

${\displaystyle 5x^{2}-5x 1=0}$

Le calcul du discriminant ${\displaystyle \Delta }$ et des racines ${\displaystyle x_{1}}$ et ${\displaystyle x_{2}}$ donne :

${\displaystyle \Delta =(-5)^{2}-4\times 5\times 1=5}$ ${\displaystyle x_{1}={5 {\sqrt {5}} \over 10}}$ et ${\displaystyle x_{2}={5-{\sqrt {5}} \over 10}}$

Dans le cas de l'équation suivante, le discriminant réduit est nul et il n'existe qu'une racine, égale à –3.

${\displaystyle x^{2} 6x 9=0}$ ${\displaystyle \Delta '=3^{2}-1\times 9=0}$ comme ${\displaystyle x^{2} 6x 9=(x 3)^{2}}$, on a ${\displaystyle x_{1}=x_{2}=-3}$

Le dernier exemple décrit une situation où le discriminant est strictement négatif, ici égal à –3. On remarque de ${\displaystyle {\rm {i}}{\sqrt {3}}}$ est une racine carrée du discriminant, si ${\displaystyle {\rm {i}}}$ désigne l'unité imaginaire. Ceci permet de déterminer les solutions :

${\displaystyle x^{2} x 1=0}$ ${\displaystyle \Delta =1^{2}-4\times 1\times 1=-3}$ ${\displaystyle x_{1}=-{1 \over 2} {\rm {i}}{{\sqrt {3}} \over 2}}$ et ${\displaystyle x_{2}=-{1 \over 2}-{\rm {i}}{{\sqrt {3}} \over 2}}$

On peut remarquer que ces deux racines sont des racines de l'unité : elles ont pour cube (pour puissance troisième) le nombre 1. Le polynôme choisi est un cas particulier de polynôme cyclotomique.

Le nombre d'or est l'unique solution positive de l'équation ${\displaystyle x^{2}=x 1}$ : ici ${\displaystyle \Delta =5}$, donc ${\displaystyle \varphi ={1 {\sqrt {5}} \over 2}}$.

Interprétation géométrique

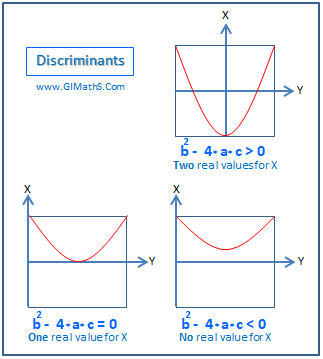
L'équation ${\displaystyle ax^{2} bx c=y.}$ définit (pour ${\displaystyle a}$ non nul) une parabole, et rechercher la solution ${\displaystyle y=0}$ revient à rechercher l'intersection de cette parabole avec l'axe des abscisses. Le discriminant permet de savoir si cette intersection existe, selon les trois possibilités illustrées par l'image en haut de l'article :

• courbe bleue (discriminant positif) : la parabole croise deux fois l'axe des abscisses ; pour ${\displaystyle x}$ entre les deux solutions, ${\displaystyle y}$ a le signe opposé à ${\displaystyle a}$, et le même signe que ${\displaystyle a}$ à l'extérieur ;
• courbe rouge (discriminant nul) : la parabole tangente l'axe des abscisses en un point unique (la solution double) ;
• courbe jaune (discriminant négatif) : la parabole ne croise pas l'axe des abscisses, ${\displaystyle y}$ est toujours du même signe que ${\displaystyle a}$.

Le cas des formes quadratiques en dimension 2

Sur l'ensemble des nombres réels, une forme quadratique ${\displaystyle \varphi }$ en dimension 2 associe à deux variables ${\displaystyle x}$ et ${\displaystyle y}$ un nombre à l'aide du polynôme à deux variables suivant :

${\displaystyle \varphi (x,y)=ax^{2} bxy cy^{2}\quad {\text{avec}}\quad a,b,c\in \mathbb {R} }$

Une forme quadratique possède aussi une expression matricielle :

${\displaystyle \varphi (x,y)={\begin{pmatrix}x&y\end{pmatrix}}{\begin{pmatrix}a&{\frac {b}{2}}\\{\frac {b}{2}}&c\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}$

Le déterminant de l'expression matricielle est égal à ${\displaystyle -(b^{2}-4ac)/4}$ ; on retrouve une expression proche de la précédente. Un changement de base, à l'aide d'une matrice de passage ${\displaystyle P}$ modifie la valeur du déterminant. Plus exactement la valeur dans la nouvelle base est égale à la valeur dans l'ancienne base que multiplie le carré du déterminant de ${\displaystyle P}$, le signe du déterminant reste invariant. Cette propriété est analysée dans l'article détaillé.

Pour cette raison, il existe trois définitions différentes du discriminant d'une forme quadratique en dimension deux. Le discriminant d'une forme quadratique dans une base ${\displaystyle B}$ est le déterminant de la matrice associée à la forme quadratique dans la base ${\displaystyle B}$. L'analogie avec la situation précédente permet de définir le discriminant de la forme quadratique comme étant égal à ${\displaystyle b^{2}-4ac}$. Enfin, comme le seul invariant associé au déterminant de la forme quadratique, le discriminant est aussi défini comme le signe du déterminant qui peut prendre les valeurs 1, 0 ou –1.

Le discriminant sépare les formes quadratiques en trois familles. En dimension deux, avec pour définition du discriminant la valeur du déterminant dans la base canonique, si le discriminant est de signe positif pour une valeur ${\displaystyle a}$ donnée l'ensemble ${\displaystyle E_{a}}$ des points ${\displaystyle (x,y)}$ vérifiant ${\displaystyle \varphi (x,y)=a}$ correspond à une ellipse ou à l'ensemble vide. Si le discriminant est nul, alors l'ensemble ${\displaystyle E_{a}}$ correspond à une parabole. Si le discriminant est négatif, ${\displaystyle E_{a}}$ est une hyperbole. Les formes quadratiques permettent ainsi d'obtenir les trois différentes formes de coniques.

Polynômes de degré quelconque

Le calcul des racines d'un polynôme à l'aide du discriminant ne se généralise pas aux degrés supérieurs à deux. Le discriminant d'un polynôme garde néanmoins une utilité.

Dans le cas des équations de degré deux, le discriminant est nul si et seulement si le polynôme possède une racine multiple. L'existence de racine multiple peut avoir d'importantes conséquences. En algèbre linéaire, la présence d'une racine multiple du polynôme minimal d'un endomorphisme modifie sa nature, interdisant la diagonalisation. Sur les extensions des nombres rationnels, les polynômes irréductibles, c'est-à-dire ceux qui ne sont pas factorisables, n'ont jamais de racines multiples (cf. l'article Extension séparable), cette situation n'est pas vraie pour tous les corps. Dans le cadre de la théorie de Galois, cette distinction est importante, les résultats sont différents selon la configuration.

Définition et propriétés

Dans ce paragraphe ${\displaystyle A}$ désigne un anneau intègre et ${\displaystyle P}$ un polynôme de degré ${\displaystyle n}$ dont les coefficients appartiennent à ${\displaystyle A}$ et sont notés de la manière suivante :

${\displaystyle P=a_{n}X^{n} a_{n-1}X^{n-1} \cdots a_{1}X a_{0}\;{\text{et}}\quad a_{n}\neq 0}$

La dérivée formelle de ${\displaystyle P}$ est notée ${\displaystyle P^{\prime }}$, elle existe même si ${\displaystyle A}$ est différent du corps des nombres réels ou complexes. Enfin ${\displaystyle R}$ désigne le résultant ; c'est une application particulière qui à deux polynômes de ${\displaystyle A[X]}$ associe un élément de ${\displaystyle A}$.

• Le discriminant de ${\displaystyle P}$, en général noté ${\displaystyle \Delta (P)}$, est la valeur définie par la formule suivante lorsque ${\displaystyle \deg(P^{\prime })=n-1}$ (ce qui est toujours le cas en caractéristique 0) :

${\displaystyle \Delta (P)={\frac {(-1)^{\frac {n(n-1)}{2}}}{a_{n}}}R(P,P^{\prime })}$

Le coefficient de normalisation possède son importance ; un discriminant peut ainsi être également interprété comme un volume orienté. L'usage d'une telle approche aide à l'analyse du discriminant d'une forme quadratique ou d'un anneau de Dedekind dans le cadre de la théorie algébrique des nombres.

Certains résultats de la théorie de Galois s'appliquent au discriminant, il faut alors étendre l'anneau ${\displaystyle A}$ des coefficients. Comme ${\displaystyle A}$ est commutatif unitaire intègre, il possède un corps des fractions ${\displaystyle F}$ commutatif et ${\displaystyle P}$ peut être considéré comme un polynôme à coefficients dans ${\displaystyle F}$. Ici ${\displaystyle K}$ désigne le corps de décomposition de ${\displaystyle P}$, c'est-à-dire le plus petit corps contenant ${\displaystyle F}$ et toutes les racines de ${\displaystyle P}$, à un isomorphisme près. Le discriminant possède la propriété suivante :

• Le discriminant du polynôme ${\displaystyle P}$ est non nul si et seulement si ${\displaystyle P}$ est séparable (c'est-à-dire n'admet aucune racine multiple).

Ce résultat est une conséquence d'une propriété générale du résultant de deux polynômes : il est non nul si et seulement si les deux polynômes sont premiers entre eux. Il peut aussi se déduire de la formule suivante :

• Soit ${\displaystyle \alpha _{i}}$ pour ${\displaystyle i}$ variant de 1 à ${\displaystyle n}$, les racines du polynôme ${\displaystyle P}$, le discriminant vérifie l'égalité suivante :

${\displaystyle \Delta (P)=a_{n}^{2n-2}\prod _{i$

Exemples

Le discriminant d'un polynôme de degré 1 est toujours égal à 1.

Pour les polynômes du second degré et avec les notations du premier paragraphe, on obtient :

${\displaystyle \Delta (P)={\frac {(-1)^{\frac {2(2-1)}{2}}}{a}}{\begin{vmatrix}a&2a&0\\b&b&2a\\c&0&b\\\end{vmatrix}}=-{\begin{vmatrix}1&2&0\\b&b&2a\\c&0&b\\\end{vmatrix}}=-{\begin{vmatrix}b&2a\\0&b\\\end{vmatrix}} 2{\begin{vmatrix}b&2a\\c&b\\\end{vmatrix}}=b^{2}-4ac}$

en caractéristique différente de 2 ; on retrouve bien la définition élémentaire du premier paragraphe.

Pour les polynômes de degré trois on considère généralement le polynôme normalisé, c'est-à-dire celui dont le monôme dominant est égal à 1. Avec les notations suivantes :

${\displaystyle P=X^{3} aX^{2} bX c}$

on obtient, si ${\displaystyle A=\mathbb {Q} }$ :

${\displaystyle \Delta (P)=(-1)^{\frac {3(3-1)}{2}}{\begin{vmatrix}1&a&b&c&0\\0&1&a&b&c\\3&2a&b&0&0\\0&3&2a&b&0\\0&0&3&2a&b\\\end{vmatrix}}=a^{2}b^{2} 18abc-4b^{3}-4a^{3}c-27c^{2}}$

L'expression est un peu complexe ; pour cette raison, la tradition est de réaliser des substitutions. On obtient le résultat général suivant : supposons que ${\displaystyle A}$ est un corps commutatif de caractéristique différente de 2 et de 3. Alors on peut mettre le polynôme unitaire ${\displaystyle P(X)\in A[X]}$ sous la forme :

${\displaystyle P=X^{3} pX q\quad {\text{et}}\quad \Delta (P)=-2^{2}p^{3}-3^{3}q^{2}}$

Dans le cas d'une équation polynomiale de degré 3 à coefficients réels, si ce discriminant est strictement positif, l'équation admet trois solutions réelles distinctes, si ce discriminant est nul, une racine est multiple et toutes sont réelles, si ce discriminant est strictement négatif, l'équation n'admet qu'une solution réelle, les deux autres sont complexes conjuguées. Par exemple, pour l'équation binomiale ${\displaystyle X^{3}-a=0}$, ce discriminant vaut ${\displaystyle -27a^{2}<0}$ si ${\displaystyle a}$ est un réel non nul.

Les solutions de l'équation ${\displaystyle X^{3} pX q=0}$ sur un corps commutatif ${\displaystyle K}$ de caractéristique différente de 2 et de 3 sont données par la « formule de Cardan » qu'on peut, dans une clôture algébrique de ${\displaystyle K}$, mettre sous la forme

${\displaystyle {\rm {j}}^{k}{\sqrt[{3}]{{1 \over 2}\left(-q {\sqrt {\frac {-\Delta }{3^{3}}}}\right)}} {\rm {j}}^{-k}{\sqrt[{3}]{{1 \over 2}\left(-q-{\sqrt {\frac {-\Delta }{3^{3}}}}\right)}}}$

${\displaystyle \left(0\leq k\leq 2\right)}$ où ${\displaystyle \Delta }$ est le discriminant noté ci-dessus ${\displaystyle \Delta (P)}$ et ${\displaystyle {\rm {j}}}$ est une racine cubique primitive de l'unité (valant donc ${\displaystyle e^{\frac {2i\pi }{3}}}$ si ${\displaystyle K=\mathbb {C} }$). Les deux termes ${\displaystyle u_{k}}$ et ${\displaystyle v_{k}}$ de cette somme sont liés par la relation ${\displaystyle 3u_{k}v_{k}=-p}$. On trouvera un exemple de résolution d'équation du troisième degré en caractéristique finie à l'article Méthode de Cardan.

Les courbes elliptiques sont un cas particulier de polynômes du troisième degré à deux variables. Pour le cas simple d'une courbe elliptique de la forme ${\displaystyle y^{2}=x^{3} px q}$, où les coefficients ${\displaystyle q,p}$ sont des nombres réels, le discriminant est de nouveau défini par ${\displaystyle \Delta =-4p^{3}-27q^{2}}$.

Expression générale

L'expression générale du discriminant du polynôme ${\displaystyle P}$ défini par :

${\displaystyle P=a_{n}X^{n} a_{n-1}X^{n-1} \cdots a_{1}X a_{0}\;}$

est la suivante :

et après simplification du coefficient ${\displaystyle a_{n}}$ sur la première ligne du déterminant, afin d'obtenir une définition valable sur tout anneau commutatif :

Utilisations du discriminant

• On a vu que dans le cas d'équations du second ou du troisième degré, le discriminant permet de calculer les racines et son signe permet de les caractériser. Considérons plus généralement un polynôme ${\displaystyle f\left(X\right)}$ à coefficients réels de degré ${\displaystyle n>0}$. Si les racines de ce polynôme sont toutes réelles et distinctes, son discriminant ${\displaystyle \Delta }$ vérifie ${\displaystyle \Delta >0}$. Si ${\displaystyle \Delta <0}$, les racines de ${\displaystyle f\left(X\right)}$ sont distinctes et deux d'entre elles au moins sont complexes conjuguées. Plus généralement, soit ${\displaystyle k}$ un corps commutatif et ${\displaystyle f\left(X\right)\in k\left[X\right]}$ un polynôme de degré ${\displaystyle \geq 2}$. Si les racines de ${\displaystyle f\left(X\right)}$ dans une clôture algébrique de ${\displaystyle k}$ appartiennent à ${\displaystyle k}$, le discriminant est un carré dans ${\displaystyle k}$.

• Soit ${\displaystyle k}$ un corps commutatif et ${\displaystyle f\left(X\right)\in k\left[X\right]}$ un polynôme de degré ${\displaystyle \geq 2}$. Ce polynôme est séparable si, et seulement si son discriminant ${\displaystyle \Delta }$ est ${\displaystyle \neq 0}$.
• Soit ${\displaystyle k}$ un corps commutatif de caractéristique ${\displaystyle \neq 2}$, ${\displaystyle f\left(X\right)\in k\left[X\right]}$ un polynôme séparable de degré ${\displaystyle n\geq 2}$, ${\displaystyle E\supseteq k}$ son corps de décomposition, et ${\displaystyle \alpha _{1},...,\alpha _{n}}$ les racines de ${\displaystyle f}$ dans ${\displaystyle E}$. Les conditions suivantes sont équivalentes :

(a) Le groupe de Galois ${\displaystyle G\left(E/k\right)}$, en tant que groupe des permutations de ${\displaystyle \alpha _{1},...,\alpha _{n}}$, est inclus dans le groupe alterné ${\displaystyle A_{n}}$.

(b) ${\displaystyle \delta =\prod \nolimits _{i$ appartient à ${\displaystyle k}$.

(c) Le discriminant ${\displaystyle \Delta }$ est un carré dans ${\displaystyle k}$.

Discriminant d'un anneau d'entiers algébriques

La théorie algébrique des nombres utilise la notion de discriminant à partir d'une définition qui semble différente : elle correspond à un déterminant d'une forme quadratique et s'applique à un anneau commutatif ${\displaystyle A}$. Les deux définitions sont néanmoins intimement corrélées. S'il existe un entier algébrique ${\displaystyle a}$ tel que l'anneau ${\displaystyle A}$ est égal à ${\displaystyle \mathbb {Z} [a]}$ — ici ${\displaystyle \mathbb {Z} }$ désigne les entiers relatifs — alors le polynôme minimal de ${\displaystyle a}$ est à coefficients dans ${\displaystyle \mathbb {Z} }$. Son discriminant au sens des polynômes est égal au discriminant de l'anneau au sens de la théorie algébrique des nombres.

Notes et références

Bibliographie

• Nicolas Bourbaki, Algèbre, Chapitres 4 à 7, Springer, 2006, 432 p. (ISBN 3-540-34398-9).
• (en) Paul Moritz Cohn, Basic Algebra, Springer, 2005, 480 p. (ISBN 81-8128-047-4).
• Serge Lang, Algèbre [détail des éditions].
• (en) Saunders Mac Lane et Garrett Birkhoff, Algebra, AMS, 1999, 3^e éd., 626 p. (ISBN 0-8218-1646-2, lire en ligne).
• Pierre Samuel, Théorie algébrique des nombres [détail de l’édition].
• Daniel Perrin, Cours d'algèbre [détail des éditions].
• (en) Robert J. Walker, Algebraic curves, Springer, 1978 (ISBN 978-03-879-0361-3).

• Portail de l’algèbre